Kalman Filter

Proof of Kalman Filter

Linear System

The figure below shows a discrete-time linear system.

Discrete-time linear system

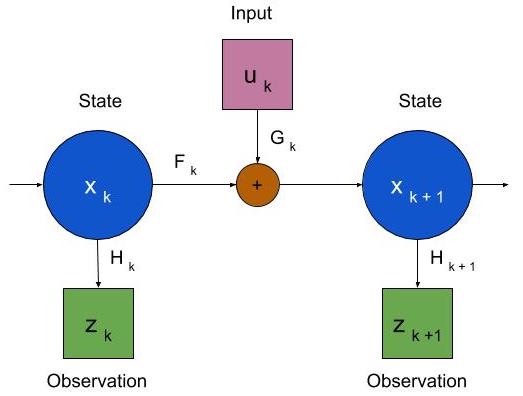
$k$ represents the discrete time instants. $\x$, $u_k$ and $z_k$ represent the state of the system, input to the system and measurement of the system at time $k$ respectively. The system is governed by the following equations -

\[\begin{aligned} \xx &= \F \x + \G u_k + w_k & \text{(State Equation)} \\ \zz &= \H \xx + v_{k+1} & \text{(Sensor Equation)} \end{aligned}\]

$w_k$ is the modeling noise of the state and $v_k$ is the measurement noise of the sensors. $x$, $z$, $w$ and $v$ are random variables, and $u$, $F$, $G$ and $H$ are deterministic. The task of filtering is to obtain an estimate of state $\x$, given observations $z_1, z_2, ..., z_k$. The Kalman filter is a linear unbiased estimator which minimizes the mean squared error. We present the proof of Kalman filter here for a discrete-time linear system.

Notations

We use the following notations:

\[\begin{aligned} Z_k &= z_1, z_2, ..., z_k\\ \hat{x}_{k|j} &= E[x_k | Z_j]\\ P_{k|j} &= Var[x_k|Z_j] = \cvar{x_k - \hat{x}_{k|j}}{Z_j} \end{aligned}\]

Assumptions

We assume the following:

$w_k$ and $v_k$ are zero-mean white noise.
\[\begin{aligned} E[w_k] &= \mathbf{0}\\ E[v_k] &= \mathbf{0}\\ Cov[w_k,w_l] = E[w_k w_l^T] &= \begin{cases} \Q & k = l \\ \mathbf{0} & k \neq l \end{cases}\\ Cov[v_k,v_l] = E[v_k v_l^T] &= \begin{cases} R_k & k = l \\ \mathbf{0} & k \neq l \end{cases} \end{aligned}\]
$\Q$ and $R_k$ are symmetric positive-definite matrices.
$w_k$ and $v_k$ are uncorrelated with $\x$ and $Z_k$.
$E[x_0] = x_{0|0}$ and $Var[x_0] = \var{x_0 - x_{0|0}} = P_{0|0}$ are the given initial state conditions. $x_0$ is uncorrelated with $w_0$ and $v_0$.

Kalman Filter

Kalman filter gives a recursive formula for the estimates in prediction and update steps.

Prediction

\[\begin{aligned} \prex &= \F \hat{x}_{k|k} + \G u_k \\ \preP &= \F P_{k|k} \F^T + \Q \end{aligned}\]

Update

\[\begin{aligned} \K &= \preP \H^T (\H \preP \H^T + \R)^{-1} \\ \postx &= \prex + \K (\zz - \H \prex) \\ \postP &= (I - \K \H) \preP \end{aligned}\]

The Kalman filter propagates the conditional mean and variance of the state, by expressing $\postx$ and $\postP$ in terms of $\hat{x}_{k|k}$ and $P_{k|k}$.

$\prex$ is the prior estimate of $\xx$ before observing $\zz$, and $\postx$ is the posterior estimate of $\xx$ after the measurement $\zz$ of the state. Similarly $\preP$ and $\postP$ are the prior and posterior estimates of the variance of the state.

$\K$ is called the Kalman Gain at time $k + 1$, because it weighs the information gained from the measurement $\zz$ by taking its difference with the predicted measurement $\H \prex$.

We prove three lemmas in the next section, two of which involve taking the gradient of trace operations and the other concerns with uncorrelated random variables. We use those to prove the Kalman Filter equations in section.

Lemmas

Lemma 1

$E[(X + Y)(X + Y)^T] = E[XX^T] + E[YY^T]$, if $X$ and $Y$ are uncorrelated, and one of $E[X]$ or $E[Y]$ is 0.

Proof

Proof

$X$ and $Y$ are uncorrelated, therefore $E[XY^T] = E[X]E[Y^T]$.
One of $E[X]$ or $E[Y]$ equals 0, therefore $E[XY^T] = 0$.

Similarly, $E[YX^T] = 0$.

Expanding $E[(X + Y)(X + Y)^T]$,

\[\begin{aligned} E[(X + Y)(X + Y)^T] &= E[XX^T] + E[YY^T] + E[XY^T] + E[YX^T] \\ &= E[XX^T] + E[YY^T] \qquad (E[XY^T] = E[YX^T] = 0) \end{aligned}\]

Therefore $E[(X + Y)(X + Y)^T] = E[XX^T] + E[YY^T]$.

Lemma 2

\[\nabla_A \mathbf{Tr}(AB) = B^T\]

Proof

Proof

Let $A = [a]_{n \times p}$ and $B = [b]_{p \times n}$.

\[\begin{aligned} \mathbf{Tr}(AB) &= \sum_{k=1}^{n} (AB)_{kk} = \sum_{k=1}^{n} \sum_{l=1}^{p} a_{kl} b_{lk} \end{aligned}\]

Taking gradient with respect to $a_{ij}$,

\[\begin{aligned} \part \mathbf{Tr}(AB) &= \part \sum_{k=1}^{n} \sum_{l=1}^{p} a_{kl} b_{lk} = \sum_{k=1}^{n} \sum_{l=1}^{p} \part a_{kl} b_{lk} \\ &= \part a_{ij} b_{ji} = b_{ji} \end{aligned}\]

Therefore $\nabla_A \mathbf{Tr}(AB) = B^T$.

Lemma 3

\[\nabla_A \mathbf{Tr}(ABA^T) = A(B + B^T) \overset{B = B^T}{=} 2AB\]

Proof

Proof

Let $A = [a]_{n \times p}$ and $B = [b]_{p \times p}$.

\[\begin{aligned} \mathbf{Tr}(ABA^T) &= \sum_{k=1}^{n} (ABA^T)_{kk} \\ &= \sum_{k=1}^{n} \sum_{l=1}^{p} a_{kl} (BA^T)_{lk}\\ &= \sum_{k=1}^{n} \sum_{l=1}^{p} a_{kl} \sum_{r=1}^{p} b_{lr} (A^T)_{rk}\\ &= \sum_{k=1}^{n} \sum_{l=1}^p \sum_{r=1}^p a_{kl} b_{lr} a_{kr} \end{aligned}\]

Taking gradient with respect to $a_{ij}$,

\[\begin{aligned} \part \mathbf{Tr} (ABA^T) &= \part \sum_{k=1}^{n} \sum_{l=1}^p \sum_{r=1}^p a_{kl} b_{lr} a_{kr} \\ &= \sum_{k=1}^{n} \sum_{l=1}^p \sum_{r=1}^p \part a_{kl} b_{lr} a_{kr} \\ &= \sum_{l=1}^p \sum_{r=1}^p \part a_{il} b_{lr} a_{ir} \\ &= \part a_{ij}^2 b_{jj} + \sum_{l=1, l \neq j}^p \part a_{il} b_{lj} a_{ij} + \sum_{r=1, r \neq j}^p \part a_{ij} b_{jr} a_{ir} \\ &= 2 a_{ij} b_{ij} + \sum_{l=1, l \neq j}^p a_{il}b_{lj} + \sum_{r=1,r \neq j}^p b_{jr} a_{ir} \\ &= \sum_{l=1}^p a_{il} b_{lj} + \sum_{r=1}^p a_{ir}b_{jr} \end{aligned}\]

Therefore,

\[\begin{aligned} \nabla_A \mathbf{Tr} (ABA^T) &= AB + AB^T \\ &= 2AB \quad \text{if } B = B^T \end{aligned}\]

Proof

We prove the prediction and update equations of Kalman Filter.

Let us rewrite the equations governing the discrete-time linear system.

\[\begin{align} \xx &= \F \x + \G u_k + w_k & \text{(State Equation)} \label{state} \\ \zz &= \H \xx + v_{k+1} & \text{(Sensor Equation)} \label{sensor} \end{align}\]

We find $\prex$ using the Kalman Filter state equation.

\[\begin{align} \nonumber \prex &= E[x_{k+1} | Z_k] \\ \nonumber &= E[\F \x + \G u_k + w_k | Z_k] & \text{(using Eq \ref{state})} \\ \nonumber &= \F E[\x | Z_k] + \G u_k + E[w_k | Z_k] & \text{($u_k$ is not random)} \\ \nonumber &= \F E[x_k | Z_k] + \G u_k & (E[w_k] = 0) \\ &= \F \hat{x}_{k|k} + \G u_k & \text{(definition of $\hat{x}_{k|k}$)} \label{prex} \end{align}\]

We substitute $\prex$ in the definition of $\preP$ using equation \ref{prex}.

\[\begin{align} \nonumber \preP &= \cvar{\xx - \prex}{Z_k} \\ \nonumber &= \cvarbreaktwo{\F \x + \G u_k + w_k - \F \hat{x}_{k|k} - \G u_k}{Z_k} \\ \nonumber & \qquad \text{(substituting $\xx$ and $\prex$ using Eq \ref{state} and Eq \ref{prex} resp.)} \\ \nonumber &= \cvar{\F (\x - \hat{x}_{k|k}) + w_k}{Z_k} \end{align}\]

From definition, we know that $\hat{x}_{k|k} = g(Z_k)$ for some function $g$, and $w_k$ is uncorrelated with $Z_k$ and $x_k$.

Therefore $w_k$ is uncorrelated with $\F (\x - \hat{x}_{k|k})$. $E[w_k] = 0$, and we can use Lemma 1.

\[\begin{align} \nonumber \preP &= \cvar{\F (\x - \hat{x}_{k|k}) + w_k}{Z_k} \\ \nonumber &= \F \cvar{\x - \hat{x}_{k|k}}{Z_k} \F^T + E[w_k w_k^T | Z_k] & \text{(using Lemma 1)} \\ \nonumber &= \F P_{k|k} \F^T + \Q & \text{(definition of $P_{k|k}$ and $\Q$)} \end{align}\]

Kalman filter is an unbiased linear optimal estimator. This implies the following:

Unbiased - The expected value of an unbiased estimator equals the expected value of the parameter. Therefore, $E[\postx] = E[\xx]$ and $E[\hat{x}_{k|k}] = E[\x]$.
Linear - A linear estimator means it is a linear combination of the observations, which in this case is $Z_{k+1}$.

$\prex$ is a function of $Z_k$. Therefore let $\postx = \KK\prex + \K \zz$, for some matrix $\KK$ and $\K$.
Optimal - The estimator minimizes the mean squared error. Therefore, $\postx = argmin \; E[(\xx - \postx)^T(\xx - \postx) | \ZZ]$.

We use these three conditions to find $\K$ and $\KK$.

\[\begin{align} \nonumber E[\xx] &= E[\postx] & \text{($\postx$ is unbiased)} \\ \nonumber &= E[\KK\prex + \K \zz] & \text{($\postx$ is a linear estimator)} \\ \nonumber \nonumber &= \KK E[\F \hat{x}_{k|k} + \G u_k] + \K E[\H \xx + v_{k+1}] \\ \nonumber &\qquad \text{(substituting $\zz$ and $\prex$ using Eq \ref{sensor} and Eq \ref{prex} resp.)} \\ \nonumber &= \KK (\F E[\hat{x}_{k|k}] + \G u_k) + \K \H E[\xx] & (E[v_{k+1}] = 0) \\ \nonumber &= \KK (\F E[\x] + \G u_k) + \K \H E[\xx] & \text{($\hat{x}_{k|k}$ is unbiased)} \\ \nonumber &= \KK E[\F x_k + \G u_k + w_k] + \K \H E[\xx] & (E[w_k] = 0) \\ \nonumber &= \KK E[\xx] + \K \H E[\xx] & \text{(using Eq \ref{state})} \\ \nonumber &= (\KK + \K \H) E[\xx] \\ \nonumber I &= \KK + \K \H \\ \KK &= I - \K \H \label{kdash} \end{align}\]

Substituting $\KK$ in the expression of $\postx$,

\[\begin{align} \nonumber \postx &= \KK \prex + \K \zz \\ \nonumber &= (I - \K \H) \prex + \K \zz & \text{(using Eq \ref{kdash})} \\ &= \prex + \K (\zz - \H \prex) \label{postx} \end{align}\]

We substitute $\postx$ in the definition of $\postP$ using equation \ref{postx},

\[\begin{align} \nonumber \postP &= \cvar{\xx - \postx}{Z_{k+1}} \\ &= \cvarbreaktwo{\xx - \prex - \K (\zz - \H \prex)}{\ZZ} \\ \nonumber &\qquad \text{(substituting $\xx$ using Eq \ref{postx})} \\ &= \cvarbreaktwo{\xx - \prex - \K (\H \xx + v_{k+1} - \H \prex)}{\ZZ} \\ \nonumber &\qquad \text{(substituting $\zz$ using Eq \ref{sensor})} \\ &= \cvarbreak{(I - \K \H) (\xx - \prex) - \K v_{k+1}}{\ZZ} \end{align}\]

$\postx = g(Z_{k+1})$ for some function $g$, and $v_{k+1}$ is uncorrelated with $Z_{k+1}$ and $x_{k+1}$. Therefore $\K w_{k+1}$ is uncorrelated with $(I - \K \H) (\xx - \prex)$. $E[v_{k+1}] = 0$. Therefore we can use Lemma 1.

\[\begin{align} \nonumber \postP &= \cvarbreak{(I - \K \H) (\xx - \prex) - \K v_{k+1}}{\ZZ} \\ \nonumber &= (I - \K \H) \cvar{\xx - \prex}{\ZZ} \\ \nonumber &= (I - \K \H)^T + \K E[v_{k+1} v_{k+1}^T | \ZZ] \K^T & \text{(using Lemma 1)} \\ \nonumber \nonumber &= (I - \K \H) \preP (I - \K \H)^T + \K \R \K^T \\ &\qquad \text{(definition of $\preP$ and $\R$)} \label{postP} \end{align}\]

We find $\K$ by minimizing the conditional mean squared error of $\postx$, $L = E[(\xx - \postx)^T(\xx - \postx)|\ZZ]$.

We express $L$ as a trace of $\postP$, and use equation \ref{postP} to write it in terms of $\K$. We then minimize $L$ and find $\K$.

\[\begin{align} \nonumber L &= E[(\xx - \postx)^T(\xx - \postx) | \ZZ] \\ \nonumber &= \mathbf{Tr}(\cvar{\xx - \postx}{\ZZ}) \\ \nonumber &= \mathbf{Tr}(\postP) & \text{(definition of $\postP$)} \\ \nonumber &= \mathbf{Tr}((I - \K \H) \preP (I - \K \H)^T + \K \R K^T) & \text{(using Eq \ref{postP})} \\ \nonumber &= \mathbf{Tr}(\; \preP - \preP \H^T \K^T - \K \H \preP \\ \nonumber &\qquad + \K \H \preP \H^T \K^T + \K \R \K^T) \\ \nonumber &= \mathbf{Tr}(\preP) - \mathbf{Tr}(\preP \H^T \K^T) - \mathbf{Tr}(\K \H \preP) \\ \nonumber &\qquad + \mathbf{Tr}(\; \K (\H \preP \H^T + \R) \K^T) & \text{($\mathbf{Tr}$ is a linear operator)} \\ \nonumber &= \mathbf{Tr}(\preP) - \mathbf{Tr}(\K \H \preP) - \mathbf{Tr}(\K \H \preP) \\ \nonumber &\qquad + \mathbf{Tr}(\; \K (\H \preP \H^T + \R) \K^T) & (\mathbf{Tr}(A) = \mathbf{Tr}(A^T)) \\ \nonumber &= \mathbf{Tr}(\preP) - 2 \; \mathbf{Tr}(\K \H \preP) \\ &\qquad + \mathbf{Tr}(\; \K (\H \preP \H^T + \R) \K^T) \label{loss} \end{align}\]

Taking the gradient of $L$ with respect to $\K$ and setting it equal to 0,

\[\begin{align} \nonumber \nabla_{\K} L &= 0 \\ \nonumber 0 &= \nabla_{\K}\; (\mathbf{Tr}(\K (\H \preP \H^T + \R) \K^T) \\ \nonumber &\qquad - 2\; \mathbf{Tr}(\K \H \preP) + \mathbf{Tr}(\preP)) & \text{(using Eq \ref{loss})} \\ \nonumber &= \nabla_{\K}\; (\mathbf{Tr}(\K (\H \preP \H^T + \R) \K^T) \\ \nonumber &\qquad - 2\; \mathbf{Tr}(\K \H \preP)) \\ \nonumber &= 2\;\K (\H \preP \H^T + \R) - 2\; \preP \H^T & \text{(using Lemma 2 and 3)} \\ \therefore\quad \K &= \preP \H^T (\H \preP \H^T + \R)^{-1} \label{kgain} \end{align}\]

We can simplify the expression of $\postP$ in equation \ref{postP} using equation \ref{kgain}.

\[\begin{align} \nonumber \postP &= (I - \K \H) \preP (I - \K \H)^T + \K \R \K^T \\ \nonumber &= \preP - \preP \H^T \K^T - \K \H \preP \\ \nonumber &\quad + \K \H \preP \H^T \K^T + \K \R \K^T \\ \nonumber &= \preP - \preP \H^T \K^T - \K \H \preP \\ \nonumber &\quad + \K (\H \preP \H^T + \R) \K^T \\ \nonumber &= \preP - \preP \H^T \K^T - \K \H \preP \\ \nonumber &\quad + \preP \H^T (\H \preP \H^T + \R)^{-1} (\H \preP \H^T + \R) \K^T \\ \nonumber &\qquad \text{(substituing $\K$ using Eq \ref{kgain})} \\ \nonumber &= \preP - \preP \H^T \K^T - \K \H \preP + \preP \H^T \K^T \\ \nonumber &= \preP - \K \H \preP \\ \nonumber &= (I - \K \H) \preP \end{align}\]

Arranging all results together,

\[\begin{aligned} \prex &= \F \hat{x}_{k|k} + \G u_k \\ \preP &= \F P_{k|k} \F^T + \Q \\ \K &= \preP \H^T (\H \preP \H^T + \R)^{-1} \\ \postx &= \prex + \K (\zz - \H \prex) \\ \postP &= (I - \K \H) \preP \end{aligned}\]